How To Create EPUB 3 Read Aloud eBooks
RSS • Permalink • Created 02 Aug 2014 • Written by Alberto Pettarin
This post describes the steps needed to create EPUB 3 eBooks with Media Overlays, also known as "read aloud" eBooks, with tips and tricks, and a full EPUB 3 demo.
Media Overlays 101
First, let me briefly recall that Media Overlays (MO) is the technical term for the part of the EPUB 3 specification specifying that the (visual) rendition of the text of the eBook must be accompanied by, and synchronized to, the (aural) rendition of some pre-recorded audio file, embedded in the eBook container.
This function is commonly called "read aloud", assuming that the words in the pre-recorded audio match the written text. (But this does not need to always be the case. For instance, an author might want to synchronize a certain portion of the text with a background music, or, for "artistic" reasons, the audio and the text might have different words.)
Usually, when reading systems support MO, they do so by activating three functions:
- the audio rendition (hopefully with dedicated audio controls),
- the synchronous highlighting of the text fragment being narrated, and
- the "tap-to-play" function, which allows the user to tap (or click) on the text, and have the aural rendition restarting from the touched (or clicked) text fragment.
How do Media Overlays work? The abstract concept is fairly simple: given a list of text fragments and a corresponding audio narration, an MO is a list of assertions like:
- "the first fragment of the text is narrated between 0s and 11s in the audio file",
- "the second fragment between 11s and 23s",
- "the third fragment between 23s and 29s", etc.
Here "fragment" might be a paragraph, a sentence, a group of words, or even a single word: it is up to the author of the eBook to decide which one suits best the intended user experience. For example, if you are crafting a children's book with slow narration, you might want to highlight single words. If you try to do the same for a "normal speed" Audio-eBook, it will result in a nasty "catch-me-if-you-can" effect, effectively forcing you to use a coarser (e.g., sentence level) granularity. Moreover, if you are going to manually produce the SMIL files, the finer the granularity, the more labor you will need to do.
The SMIL File Syntax
The EPUB 3 MO specification requires the sync information to be described using a SMIL file, similar to the following:
<smil xmlns="http://www.w3.org/ns/SMIL" xmlns:epub="http://www.idpf.org/2007/ops" version="3.0">
<body>
<seq epub:textref="p001.xhtml">
<par><text src="p001.xhtml#f001"/><audio clipBegin="00:00:00.000" clipEnd="00:00:02.680" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f002"/><audio clipBegin="00:00:02.680" clipEnd="00:00:05.480" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f003"/><audio clipBegin="00:00:05.480" clipEnd="00:00:08.640" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f004"/><audio clipBegin="00:00:08.640" clipEnd="00:00:11.960" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f005"/><audio clipBegin="00:00:11.960" clipEnd="00:00:15.279" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f006"/><audio clipBegin="00:00:15.279" clipEnd="00:00:18.519" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f007"/><audio clipBegin="00:00:18.519" clipEnd="00:00:22.760" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f008"/><audio clipBegin="00:00:22.760" clipEnd="00:00:25.719" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f009"/><audio clipBegin="00:00:25.719" clipEnd="00:00:31.239" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f010"/><audio clipBegin="00:00:31.239" clipEnd="00:00:34.280" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f011"/><audio clipBegin="00:00:34.280" clipEnd="00:00:36.960" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f012"/><audio clipBegin="00:00:36.960" clipEnd="00:00:40.640" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f013"/><audio clipBegin="00:00:40.640" clipEnd="00:00:43.600" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f014"/><audio clipBegin="00:00:43.600" clipEnd="00:00:48.000" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f015"/><audio clipBegin="00:00:48.000" clipEnd="00:00:53.280" src="../Audio/p001.mp3"/></par>
</seq>
</body>
</smil>Each of the 15 fragments in this SMIL file specifies four things:
- an identifier for the text fragment (e.g.,
f001inp001.xhtml); - the corresponding audio file (
../Audio/p001.mp3); - the begin time (
00:00:00.000); - the end time (
00:00:02.680).
In plain English, the SMIL file above says:
f001inp001.xhtmlis "active" between0sand2.680sof the playback of audio filep001.mp3,f002inp001.xhtmlis "active" between2.680sand5.480sof the playback of audio filep001.mp3,- and so on.
The SMIL representation looks a bit redundant
because the specification allows for very complex scenarios,
where you might reference multiple XHTML/audio files or
have deeper nestings of <seq> and <par> elements.
For details about Media Overlays, see the
excellent post
by Matt Garrish,
and then RTFM!
In practice, almost always you will see eBooks where each SMIL file references just one XHTML file and one audio file, with a simple, linear structure like the one in the example above:
- a
<seq>(sequence) element that specifies the serial playback of its children, and - a set of
<par>(parallel) elements, each specifying the synchronism between its<text>and<audio>children.
A Concrete Example
It is worthy to note that a "read aloud" eBook might have "Fixed Layout" or "reflowable" rendition (or is an hybrid of the two).
Suppose you want to produce a Fixed Layout EPUB 3 with the "read aloud" feature, containing the first three Sonnets of Shakespeare, read by Elizabeth Klett for LibriVox. Where do Media Overlays come into play? What files should you add to our eBook?
You need to perform the following steps, for each XHTML file you want to attach audio to:
- produce an audio file,
- add suitable
idattributes to elements in the page, one for each desired SMIL fragment, - create a SMIL file specifying the sync information between the text and the audio,
- adding the highlighting class to the CSS,
- add the suitable metadata to the OPF file of the eBook.
Step 1: Creating the audio file
I assume you have already recorded or you have been given the audio file, so I just add a few suggestions from my experience in the trenches:
- use MP3 or MP4/AAC formats;
- use 44100 Hz or 48000 Hz;
- if you are creating an Audio-eBook with hours of audio, use mono 64-128 kbps;
- if you are creating a Fixed Layout eBook, use stereo 128 kbps or better;
- if your eBook has multiple pages/chapters but you have been given a single audio file, you should consider splitting it into several audio files, one per page/chapter. You can easily do that using Audacity, a free audio editor which has a nice "split into multiple files" function. This will reduce loading time, provide better publication granularity, and potentially increase the number of reading systems capable of correctly rendering your eBook.
Step 2: Adding id attributes to the XHTML file
Now you need to decide the granularity of your SMIL fragments. As mentioned before, you can choose finer (single word) or coarser (sentence/paragraph) granularity, depending on your eBooks and the effect you want to produce. For our example, since we deal with poetry, we choose "verse" granularity.
Suppose you start with this XHTML page:
<?xml version="1.0" encoding="UTF-8"?>
<html xmlns="http://www.w3.org/1999/xhtml" xmlns:epub="http://www.idpf.org/2007/ops" lang="en" xml:lang="en">
<head>
<meta charset="utf-8"/>
<meta name="viewport" content="width=768,height=1024"/>
<link rel="stylesheet" href="../Styles/style.css" type="text/css"/>
<title>Sonnet I</title>
</head>
<body>
<div id="divTitle">
<h1>I</h1>
</div>
<div id="divSonnet">
<p>
From fairest creatures we desire increase,<br/>
That thereby beauty’s rose might never die,<br/>
But as the riper should by time decease,<br/>
His tender heir might bear his memory:<br/>
But thou contracted to thine own bright eyes,<br/>
Feed’st thy light’s flame with self-substantial fuel,<br/>
Making a famine where abundance lies,<br/>
Thy self thy foe, to thy sweet self too cruel:<br/>
Thou that art now the world’s fresh ornament,<br/>
And only herald to the gaudy spring,<br/>
Within thine own bud buriest thy content,<br/>
And tender churl mak’st waste in niggarding:<br/>
Pity the world, or else this glutton be,<br/>
To eat the world’s due, by the grave and thee.
</p>
</div>
</body>
</html>You need to insert id attributes to each verse,
possibly by creating <div> or <span> elements,
obtaining the following markup:
<?xml version="1.0" encoding="UTF-8"?>
<html xmlns="http://www.w3.org/1999/xhtml" xmlns:epub="http://www.idpf.org/2007/ops" lang="en" xml:lang="en">
<head>
<meta charset="utf-8"/>
<meta name="viewport" content="width=768,height=1024"/>
<link rel="stylesheet" href="../Styles/style.css" type="text/css"/>
<title>Sonnet I</title>
</head>
<body>
<div id="divTitle">
<h1><span id="f001">I</span></h1>
</div>
<div id="divSonnet">
<p>
<span id="f002">From fairest creatures we desire increase,</span><br/>
<span id="f003">That thereby beauty’s rose might never die,</span><br/>
<span id="f004">But as the riper should by time decease,</span><br/>
<span id="f005">His tender heir might bear his memory:</span><br/>
<span id="f006">But thou contracted to thine own bright eyes,</span><br/>
<span id="f007">Feed’st thy light’s flame with self-substantial fuel,</span><br/>
<span id="f008">Making a famine where abundance lies,</span><br/>
<span id="f009">Thy self thy foe, to thy sweet self too cruel:</span><br/>
<span id="f010">Thou that art now the world’s fresh ornament,</span><br/>
<span id="f011">And only herald to the gaudy spring,</span><br/>
<span id="f012">Within thine own bud buriest thy content,</span><br/>
<span id="f013">And tender churl mak’st waste in niggarding:</span><br/>
<span id="f014">Pity the world, or else this glutton be,</span><br/>
<span id="f015">To eat the world’s due, by the grave and thee.</span>
</p>
</div>
</body>
</html>Clearly this step requires some effort
if you have to perform it on an already existing XHTML file.
If you control your own workflow,
adding <span> and id to the markup automatically is relatively easy,
and the same goes for the splitting of the text,
based on the punctuation or XHTML elements.
(In ReadBeyond we clearly adopt the latter approach.)
Step 3: Creating the SMIL file
Now that you have the audio file and the text fragments, it is time to create the SMIL file.
Besides formatting of the actual file, which is just a matter of respecting the SMIL syntax (feel free to copy and paste from above!), the hard part of this step consists in defining the time intervals in the audio file, each containing the spoken version of the text of each text fragment.
You have two options:
- mark the time labels manually, or
- use an automated tool.
3.1 The manual approach
You will basically listen to the audio file, and create a marker each time the current fragment ends.
In principle, you can directly author the SMIL file, preparing a template like this:
<smil xmlns="http://www.w3.org/ns/SMIL" xmlns:epub="http://www.idpf.org/2007/ops" version="3.0">
<body>
<seq id="seq1" epub:textref="p001.xhtml" epub:type="bodymatter chapter">
<par id="p001"><text src="p001.xhtml#f001"/><audio clipBegin="" clipEnd="" src="../Audio/p001.mp3"/></par>
<par id="p002"><text src="p001.xhtml#f002"/><audio clipBegin="" clipEnd="" src="../Audio/p001.mp3"/></par>
<par id="p003"><text src="p001.xhtml#f003"/><audio clipBegin="" clipEnd="" src="../Audio/p001.mp3"/></par>
<par id="p004"><text src="p001.xhtml#f004"/><audio clipBegin="" clipEnd="" src="../Audio/p001.mp3"/></par>
<par id="p005"><text src="p001.xhtml#f005"/><audio clipBegin="" clipEnd="" src="../Audio/p001.mp3"/></par>
<par id="p006"><text src="p001.xhtml#f006"/><audio clipBegin="" clipEnd="" src="../Audio/p001.mp3"/></par>
<par id="p007"><text src="p001.xhtml#f007"/><audio clipBegin="" clipEnd="" src="../Audio/p001.mp3"/></par>
<par id="p008"><text src="p001.xhtml#f008"/><audio clipBegin="" clipEnd="" src="../Audio/p001.mp3"/></par>
<par id="p009"><text src="p001.xhtml#f009"/><audio clipBegin="" clipEnd="" src="../Audio/p001.mp3"/></par>
<par id="p010"><text src="p001.xhtml#f010"/><audio clipBegin="" clipEnd="" src="../Audio/p001.mp3"/></par>
<par id="p011"><text src="p001.xhtml#f011"/><audio clipBegin="" clipEnd="" src="../Audio/p001.mp3"/></par>
<par id="p012"><text src="p001.xhtml#f012"/><audio clipBegin="" clipEnd="" src="../Audio/p001.mp3"/></par>
<par id="p013"><text src="p001.xhtml#f013"/><audio clipBegin="" clipEnd="" src="../Audio/p001.mp3"/></par>
<par id="p014"><text src="p001.xhtml#f014"/><audio clipBegin="" clipEnd="" src="../Audio/p001.mp3"/></par>
<par id="p015"><text src="p001.xhtml#f015"/><audio clipBegin="" clipEnd="" src="../Audio/p001.mp3"/></par>
</seq>
</body>
</smil>and playing the audio file: as soon as the next text has been spoken, pause the audio, and fill the current time in:
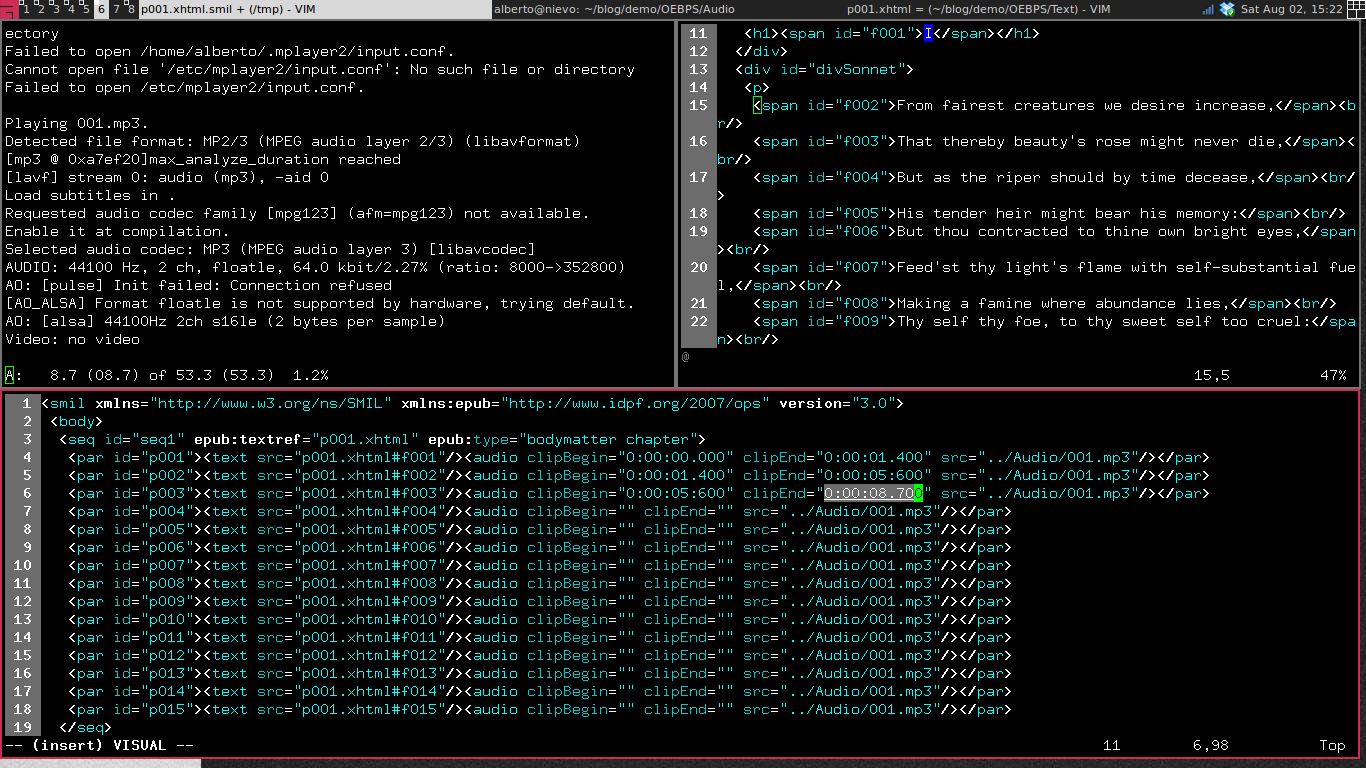
However, usually it is easier to use an audio editor which can export time labels. I will illustrate the process using Audacity, an excellent free audio editor. This is the same procedure suggested in the iBook Asset Guide.
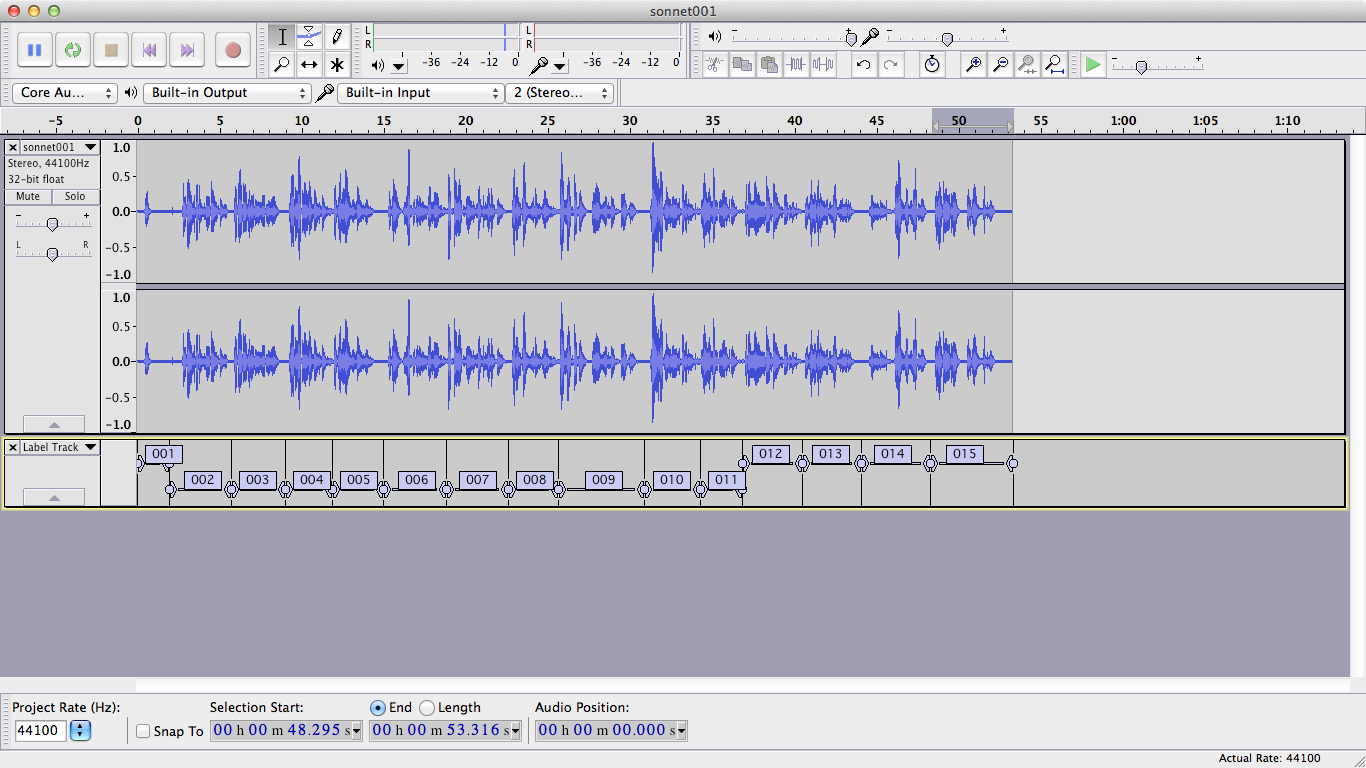
3.1.1 Open the audio file
Open the audio file (File > Open). You will see a waveform like this:
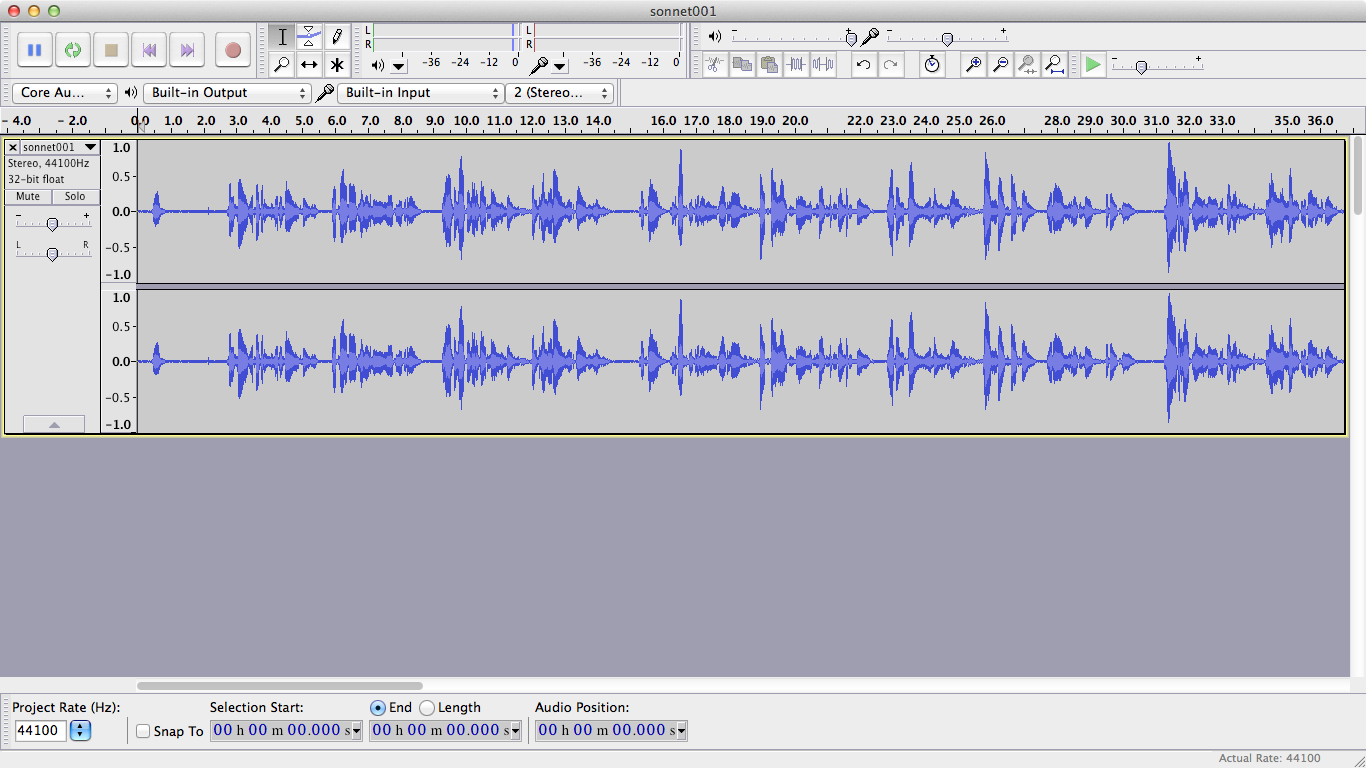
3.1.2 Create the time labels
Then, select the portion of the audio corresponding to the first text fragment.
In our case, the audio says "One" (whereas the text reads "I").
Press CTRL+B (Linux/Windows) or CMD+B (Mac) to create the label track and the first label:
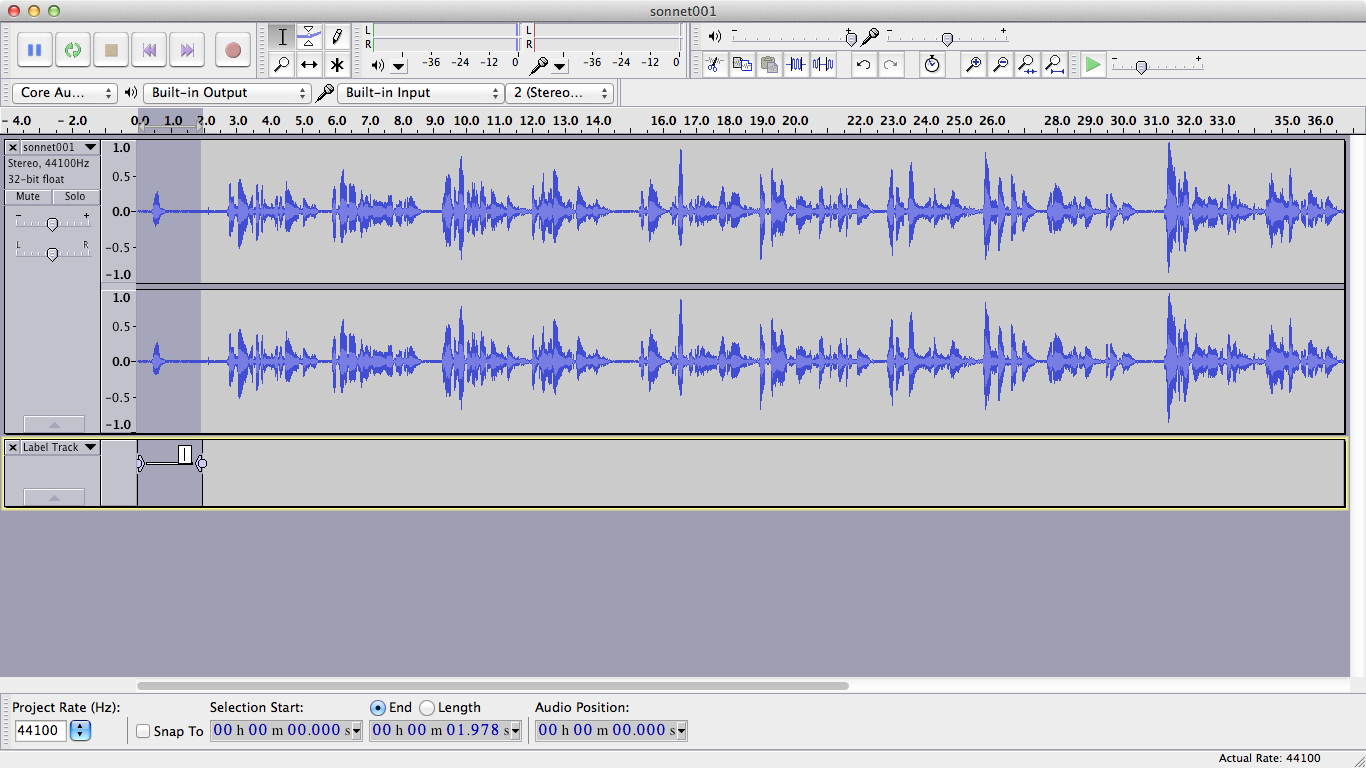
Now you can input an identifier for the selected time interval.
To make the SMIL formatting faster,
it is useful to give it the id associated text fragment
or a value from which the latter can be easily computed.
In our case, we will use 001:
(Note that our id is f001, since id must be a valid XML identifier,
and hence cannot start with a digit.
We will add the prefix f to all the fragments
when formatting the final SMIL file.)
Taking advantage of the "auto-snap" function of Audacity, which allows you to precisely start a selection from the boundary of the previous selection, keep repeating the above procedure for all the remaining fragments:
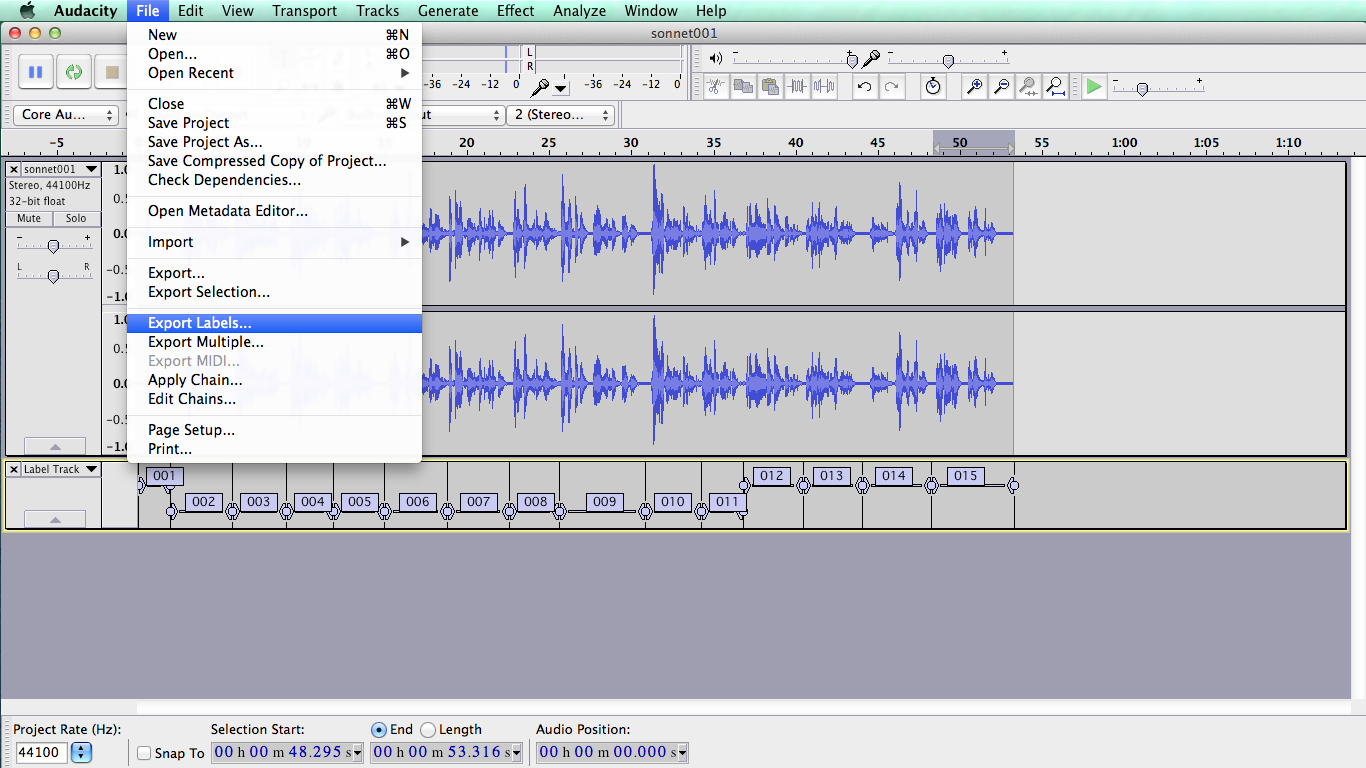
3.1.3 Export the time labels
Now you need to export the time labels. Select the menu File > Export Labels:
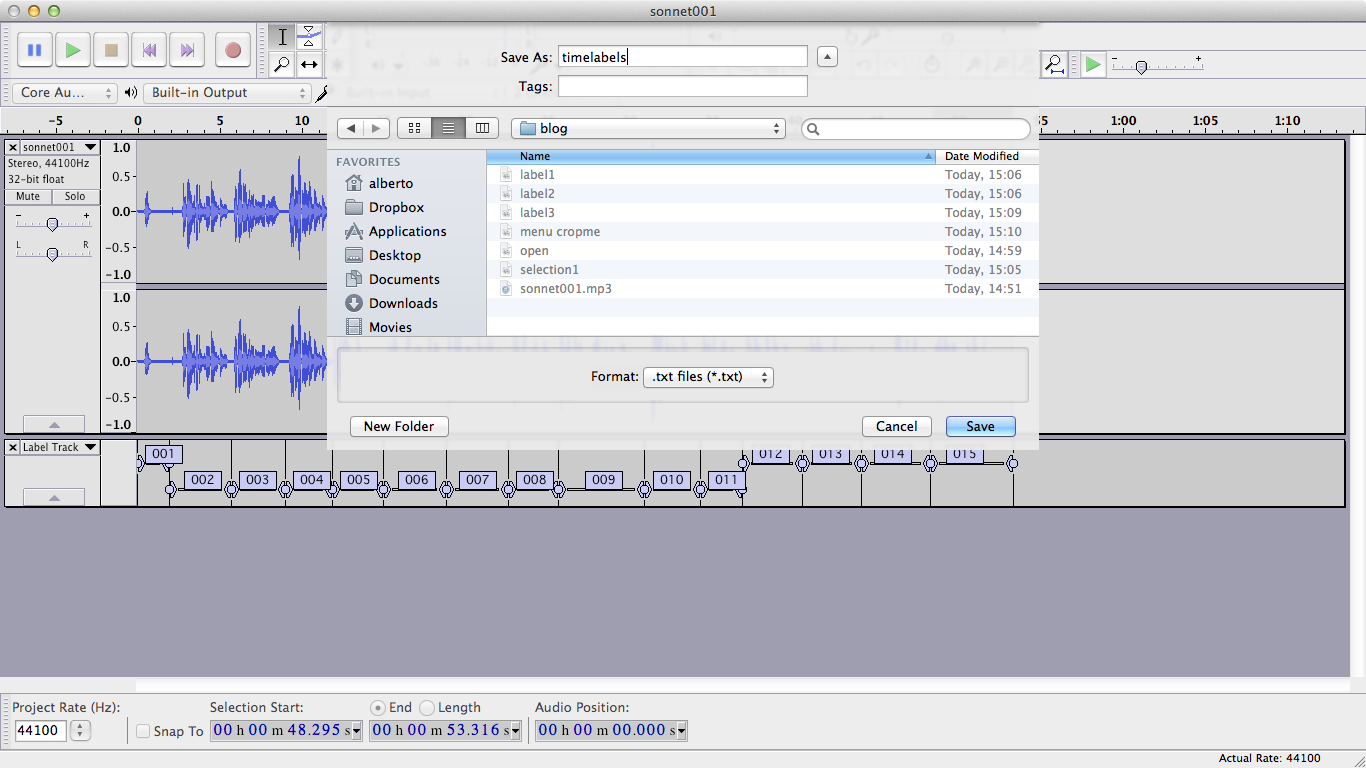
And then choose a name for the exported file, for example timelabels.txt:
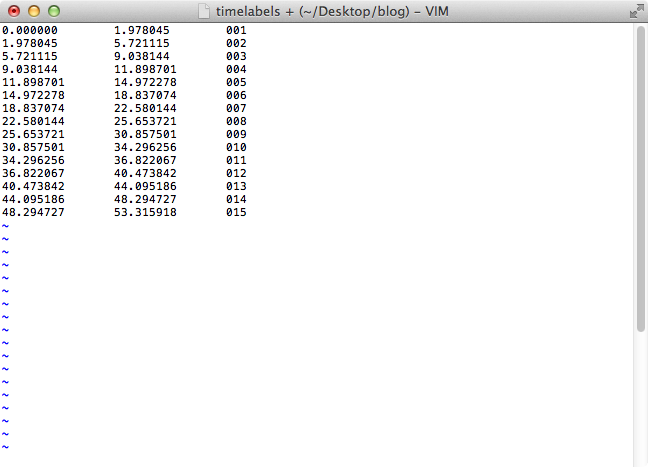
The resulting timelabels.txt is a tab-separated plain text file,
containing on each line:
- the begin of the interval (in seconds),
- the end of the interval (in seconds), and
- the label you choose.
3.1.4 Formatting the SMIL file
Formatting the SMIL file is just a regular expression away. If you use Vim, open the file of the previous step and give the command:
:%s/\(.*\)^I\(.*\)^I\(.*\)/ <par><text src="p001.xhtml#f\3"\/><audio clipBegin="\1" clipEnd="\2" src="..\/Audio\/p001.mp3"\/><\/par>
(note that ^I is the tab character), obtaining:
<par><text src="p001.xhtml#f001"/><audio clipBegin="0.000000" clipEnd="1.978045" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f002"/><audio clipBegin="1.978045" clipEnd="5.721115" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f003"/><audio clipBegin="5.721115" clipEnd="9.038144" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f004"/><audio clipBegin="9.038144" clipEnd="11.898701" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f005"/><audio clipBegin="11.898701" clipEnd="14.972278" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f006"/><audio clipBegin="14.972278" clipEnd="18.837074" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f007"/><audio clipBegin="18.837074" clipEnd="22.580144" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f008"/><audio clipBegin="22.580144" clipEnd="25.653721" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f009"/><audio clipBegin="25.653721" clipEnd="30.857501" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f010"/><audio clipBegin="30.857501" clipEnd="34.296256" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f011"/><audio clipBegin="34.296256" clipEnd="36.822067" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f012"/><audio clipBegin="36.822067" clipEnd="40.473842" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f013"/><audio clipBegin="40.473842" clipEnd="44.095186" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f014"/><audio clipBegin="44.095186" clipEnd="48.294727" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f015"/><audio clipBegin="48.294727" clipEnd="53.315918" src="../Audio/p001.mp3"/></par>Adding the header and the footer yields a working SMIL file p001.xhtml.smil:
<smil xmlns="http://www.w3.org/ns/SMIL" xmlns:epub="http://www.idpf.org/2007/ops" version="3.0">
<body>
<seq epub:textref="p001.xhtml" epub:type="bodymatter chapter">
<par><text src="p001.xhtml#f001"/><audio clipBegin="0.000000" clipEnd="1.978045" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f002"/><audio clipBegin="1.978045" clipEnd="5.721115" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f003"/><audio clipBegin="5.721115" clipEnd="9.038144" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f004"/><audio clipBegin="9.038144" clipEnd="11.898701" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f005"/><audio clipBegin="11.898701" clipEnd="14.972278" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f006"/><audio clipBegin="14.972278" clipEnd="18.837074" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f007"/><audio clipBegin="18.837074" clipEnd="22.580144" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f008"/><audio clipBegin="22.580144" clipEnd="25.653721" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f009"/><audio clipBegin="25.653721" clipEnd="30.857501" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f010"/><audio clipBegin="30.857501" clipEnd="34.296256" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f011"/><audio clipBegin="34.296256" clipEnd="36.822067" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f012"/><audio clipBegin="36.822067" clipEnd="40.473842" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f013"/><audio clipBegin="40.473842" clipEnd="44.095186" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f014"/><audio clipBegin="44.095186" clipEnd="48.294727" src="../Audio/p001.mp3"/></par>
<par><text src="p001.xhtml#f015"/><audio clipBegin="48.294727" clipEnd="53.315918" src="../Audio/p001.mp3"/></par>
</seq>
</body>
</smil>If you want a prettier output, e.g. with human-readable timings, you might want to use a more complex regex or a Python script.
Timings finer than the millisecond are generally worthless, due to the audio latency in the hardware/OS/reading system of the user device, and the human response time.
Note that Audacity is not the only choice you have, as there are other tools with a specialized GUI to help you speed the production of SMIL files up. These include TOBI (audio + EPUB 3/DAISY authoring tool, Windows only) and PubCoder (EPUB 3 FXL authoring tool, Mac only). However, both tools just provide a more "ergonomic" interface, and you still need to listen to audio and mark the labels manually.
Clearly, this approach is suitable only for a limited number of fragments. If you need to process hundreds or thousands of fragments, e.g. for Audio-eBooks, you really want to use an automated tool.
3.2 Using ReadBeyond Sync
IMPORTANT UPDATE (2015-05-25): ReadBeyond Sync was retired. The source code of the audio/text aligner has been published on GitHub, so you can use it for free on your own machine. See this post for details.
The goal of ReadBeyond Sync is to free you from the long, boring, and error-prone task of producing SMIL files. All you need to do is to upload the XHTML file, the audio file, and specify some options (the language, the output format, etc.), and hit the "Process" button.
Sync is optimized for computing SMIL files for EPUB 3 eBooks, and is designed to easily integrate into your work flow, thanks to lots of options, including flexible output and batch import of several tasks at once.
In our example, we have three XHTML pages, each with its corresponding MP3 file. The easiest way to use Sync is to create a ZIP file including the following files:
<ziproot>
config.txt
assets/
p001.xhtml
p001.mp3
p002.xhtml
p002.mp3
p003.xhtml
p003.mp3
The config.txt file contains the Sync configuration options:
is_hierarchy_type=flat
is_hierarchy_prefix=assets/
is_text_file_relative_path=.
is_text_file_name_regex=.*\.xhtml
is_text_type=unparsed
is_audio_file_relative_path=.
is_audio_file_name_regex=.*\.mp3
is_text_unparsed_id_regex=f[0-9]+
is_text_unparsed_id_sort=numeric
os_job_file_name=demo_sync_job_output
os_job_file_container=zip
os_job_file_hierarchy_type=flat
os_job_file_hierarchy_prefix=assets/
os_task_file_name=$PREFIX.xhtml.smil
os_task_file_format=smil
os_task_file_smil_page_ref=$PREFIX.xhtml
os_task_file_smil_audio_ref=../Audio/$PREFIX.mp3
job_language=en
job_description=Demo Sync Job
As you can see, it is quite straighforward to read:
it instructs Sync to parse the XHTML files in assets/,
reading the text from elements with id matching f[0-9]+,
and pairing each XHTML file with the corresponding MP3 file.
For each pair (text, audio), it will capture the name (e.g., p001) into $PREFIX,
and it will output a SMIL file named $PREFIX.xhtml.smil,
with the desired src references:
the text reference to the same directory,
while the audio reference to ../Audio/,
because we like our EPUB structured like that.
(Sync has lots of options, please see the documentation.)
Observe that you can reuse the above configuration for other project, provided that you are consistent with the naming of the files. Even modifying it on-the-fly is simple!
After processing the uploaded materials, Sync will generate a ZIP file containing:
<ziproot>
assets/
p001.xhtml.smil
p002.xhtml.smil
p003.xhtml.smil
For example, p001.xhtml.smil contains:
<smil xmlns="http://www.w3.org/ns/SMIL" xmlns:epub="http://www.idpf.org/2007/ops" version="3.0">
<body>
<seq id="s000001" epub:textref="p001.xhtml">
<par id="p000001"><text src="p001.xhtml#f001"/><audio clipBegin="00:00:00.000" clipEnd="00:00:02.680" src="../Audio/p001.mp3"/></par>
<par id="p000002"><text src="p001.xhtml#f002"/><audio clipBegin="00:00:02.680" clipEnd="00:00:05.480" src="../Audio/p001.mp3"/></par>
<par id="p000003"><text src="p001.xhtml#f003"/><audio clipBegin="00:00:05.480" clipEnd="00:00:08.640" src="../Audio/p001.mp3"/></par>
<par id="p000004"><text src="p001.xhtml#f004"/><audio clipBegin="00:00:08.640" clipEnd="00:00:11.960" src="../Audio/p001.mp3"/></par>
<par id="p000005"><text src="p001.xhtml#f005"/><audio clipBegin="00:00:11.960" clipEnd="00:00:15.279" src="../Audio/p001.mp3"/></par>
<par id="p000006"><text src="p001.xhtml#f006"/><audio clipBegin="00:00:15.279" clipEnd="00:00:18.519" src="../Audio/p001.mp3"/></par>
<par id="p000007"><text src="p001.xhtml#f007"/><audio clipBegin="00:00:18.519" clipEnd="00:00:22.760" src="../Audio/p001.mp3"/></par>
<par id="p000008"><text src="p001.xhtml#f008"/><audio clipBegin="00:00:22.760" clipEnd="00:00:25.719" src="../Audio/p001.mp3"/></par>
<par id="p000009"><text src="p001.xhtml#f009"/><audio clipBegin="00:00:25.719" clipEnd="00:00:31.239" src="../Audio/p001.mp3"/></par>
<par id="p000010"><text src="p001.xhtml#f010"/><audio clipBegin="00:00:31.239" clipEnd="00:00:34.280" src="../Audio/p001.mp3"/></par>
<par id="p000011"><text src="p001.xhtml#f011"/><audio clipBegin="00:00:34.280" clipEnd="00:00:36.960" src="../Audio/p001.mp3"/></par>
<par id="p000012"><text src="p001.xhtml#f012"/><audio clipBegin="00:00:36.960" clipEnd="00:00:40.640" src="../Audio/p001.mp3"/></par>
<par id="p000013"><text src="p001.xhtml#f013"/><audio clipBegin="00:00:40.640" clipEnd="00:00:43.600" src="../Audio/p001.mp3"/></par>
<par id="p000014"><text src="p001.xhtml#f014"/><audio clipBegin="00:00:43.600" clipEnd="00:00:48.000" src="../Audio/p001.mp3"/></par>
<par id="p000015"><text src="p001.xhtml#f015"/><audio clipBegin="00:00:48.000" clipEnd="00:00:53.280" src="../Audio/p001.mp3"/></par>
</seq>
</body>
</smil>And the best part is that you can immediately copy the generated SMIL files inside your EPUB 3 working directory and forget about SMIL authoring!
If you want to play around with Sync (which is in free Beta), these are the input and output ZIP files:
- the input ZIP
- the output ZIP
I guess I do not need to emphasize the fact that Sync is the only sane way to go, if you need to author SMIL files with hundreds or thousands of fragments, either because you have very long audio audio or you are doing word-level sync. Pause a minute, and think: do you really want to waste hours producing SMIL files, when you can use our automated tool Sync for a few bucks per hour of processed audio?
Step 4: Modifying the CSS
Great, the hardest part of the job has been done, and now you just need to add the last touches to your EPUB eBook.
The first is defining a CSS class for the MO highlighting.
For example, if you want to highlight the text with a yellow background, you can add the following:
.-epub-media-overlay-active {
background-color: #FFFF99;
}You can change the name -epub-media-overlay-active to whatever you prefer.
The mechanism is simple: once an element (i.e., a certain id)
becomes the "active" MO fragment,
the reading system adds the class -epub-media-overlay-active to it,
and it removes the same class when the element is no longer the active one.
Step 5: Modifying the OPF file
Finally, you need to add some elements and metadata to the OPF file.
5.1 Media Overlays metadata
<!--MEDIA OVERLAYS METADATA-->
<meta property="media:duration" refines="#s001">0:00:53.320</meta>
<meta property="media:duration" refines="#s002">0:00:52.950</meta>
<meta property="media:duration" refines="#s003">0:00:51.700</meta>
<meta property="media:duration">0:02:37.970</meta>
<meta property="media:narrator">Elizabeth Klett</meta>
<meta property="media:active-class">-epub-media-overlay-active</meta>In the <metadata> section of your OPF file,
you need to specify a media:duration item for each of the audio files in your eBook
(3 in our case, note the usage of refines),
and one item for its sum (the whole publication).
The value of each element is the running time of the corresponding audio.
Optionally, you can specify the name of the narrator(s) in one or more media:narrator metas;
I encourage you to do so, because reading systems can read this information and display it
to the user (e.g., Menestrello shows the narrator name in its Library View).
Although optional, you probably want to specify
the CSS class name defined in the previous section,
using the media:active-class property.
Be aware that not all reading systems properly support it,
for example Kobo apps rely on a naming convention (kobo-smil-highlight)
and ignore the value specified in the OPF file,
while other reading systems allow the user to override
the author's choice for the highlighting style
(e.g., Readium or Menestrello).
Note that media:active-class cannot be refined, as it is assumed to
apply to every MO in the publication.
Also note that EPUB 3.0.1 introduced another class media:playback-active-class,
which you can define similarily to media:active-class.
Refer to Section 3.4 of the MO specification for details.
(Moreover, I suggest we should also have media-paused-class.)
5.2 Manifest items
<item id="p001" href="Text/p001.xhtml" media-type="application/xhtml+xml" media-overlay="s001"/>
<item id="s001" href="Text/p001.xhtml.smil" media-type="application/smil+xml"/>
<item id="m001" href="Audio/p001.mp3" media-type="audio/mpeg"/>
<item id="p002" href="Text/p002.xhtml" media-type="application/xhtml+xml" media-overlay="s002"/>
<item id="s002" href="Text/p002.xhtml.smil" media-type="application/smil+xml"/>
<item id="m002" href="Audio/p002.mp3" media-type="audio/mpeg"/>
<item id="p003" href="Text/p003.xhtml" media-type="application/xhtml+xml" media-overlay="s003"/>
<item id="s003" href="Text/p003.xhtml.smil" media-type="application/smil+xml"/>
<item id="m003" href="Audio/p003.mp3" media-type="audio/mpeg"/>For each chapter/page, in the <manifest> of your OPF file you need to add:
- the
media-overlayattribute to the<item>corresponding to the XHTML document, referencing the SMIL<item>, - an
<item>for each SMIL file, and - an
<item>for each audio file.
Note that the refines of media:duration explained in the previous section
need to point to the <item> id of the SMIL elements (e.g., s001 in the example above).
Also note that the each XHTML document can be associated with at most one SMIL file.
5.3 Putting all together
You will end up with something like the following:
<?xml version="1.0" encoding="UTF-8"?>
<package xmlns="http://www.idpf.org/2007/opf" version="3.0" unique-identifier="pubID" xml:lang="en" prefix="rendition: http://www.idpf.org/vocab/rendition/#">
<metadata xmlns:dc="http://purl.org/dc/elements/1.1/" xmlns:opf="http://www.idpf.org/2007/opf">
<dc:identifier id="pubID">urn:uuid:8a5d2330-08d6-405b-a359-e6862b48ea4d</dc:identifier>
<meta refines="#pubID" property="identifier-type" scheme="xsd:string">uuid</meta>
<dc:title id="title">[DEMO] How To Create EPUB 3 Read Aloud eBooks</dc:title>
<dc:creator id="aut">Alberto Pettarin</dc:creator>
<meta refines="#aut" property="role" scheme="marc:relators">aut</meta>
<meta refines="#aut" property="file-as">Pettarin, Alberto</meta>
<dc:contributor id="nrt">Elizabeth Klett</dc:contributor>
<meta refines="#nrt" property="role" scheme="marc:relators">nrt</meta>
<meta refines="#nrt" property="file-as">Klett, Elizabeth</meta>
<dc:contributor id="bkp">ReadBeyond</dc:contributor>
<meta refines="#bkp" property="role" scheme="marc:relators">bkp</meta>
<meta refines="#bkp" property="file-as">ReadBeyond</meta>
<dc:language>it</dc:language>
<dc:date>2014-08-02</dc:date>
<meta property="dcterms:modified">2014-08-02T00:00:01Z</meta>
<meta name="cover" content="cover.png" />
<dc:publisher>ReadBeyond, Padova, Italy</dc:publisher>
<dc:rights>CC BY-NC-SA 4.0</dc:rights>
<dc:subject>William Shakespeare</dc:subject>
<dc:subject>Sonnets</dc:subject>
<dc:subject>Read aloud</dc:subject>
<dc:subject>EPUB 3 Media Overlays</dc:subject>
<dc:type>Book</dc:type>
<!--FIXED LAYOUT-->
<meta property="rendition:layout">pre-paginated</meta>
<meta property="rendition:orientation">portrait</meta>
<!--MEDIA OVERLAYS METADATA-->
<meta property="media:duration" refines="#s001">0:00:53.320</meta>
<meta property="media:duration" refines="#s002">0:00:52.950</meta>
<meta property="media:duration" refines="#s003">0:00:51.700</meta>
<meta property="media:duration">0:02:37.970</meta>
<meta property="media:narrator">Elizabeth Klett</meta>
<meta property="media:active-class">-epub-media-overlay-active</meta>
</metadata>
<manifest>
<item id="toc" href="Text/toc.xhtml" media-type="application/xhtml+xml" properties="nav"/>
<item id="cover" href="Text/cover.xhtml" media-type="application/xhtml+xml"/>
<item id="cover.png" href="Images/cover.png" media-type="image/png" properties="cover-image" />
<item id="c001" href="Styles/style.css" media-type="text/css"/>
<item id="p001" href="Text/p001.xhtml" media-type="application/xhtml+xml" media-overlay="s001"/>
<item id="s001" href="Text/p001.xhtml.smil" media-type="application/smil+xml"/>
<item id="m001" href="Audio/p001.mp3" media-type="audio/mpeg"/>
<item id="p002" href="Text/p002.xhtml" media-type="application/xhtml+xml" media-overlay="s002"/>
<item id="s002" href="Text/p002.xhtml.smil" media-type="application/smil+xml"/>
<item id="m002" href="Audio/p002.mp3" media-type="audio/mpeg"/>
<item id="p003" href="Text/p003.xhtml" media-type="application/xhtml+xml" media-overlay="s003"/>
<item id="s003" href="Text/p003.xhtml.smil" media-type="application/smil+xml"/>
<item id="m003" href="Audio/p003.mp3" media-type="audio/mpeg"/>
</manifest>
<spine page-progression-direction="ltr">
<itemref idref="cover" linear="yes"/>
<itemref idref="p001" linear="yes"/>
<itemref idref="p002" linear="yes"/>
<itemref idref="p003" linear="yes"/>
</spine>
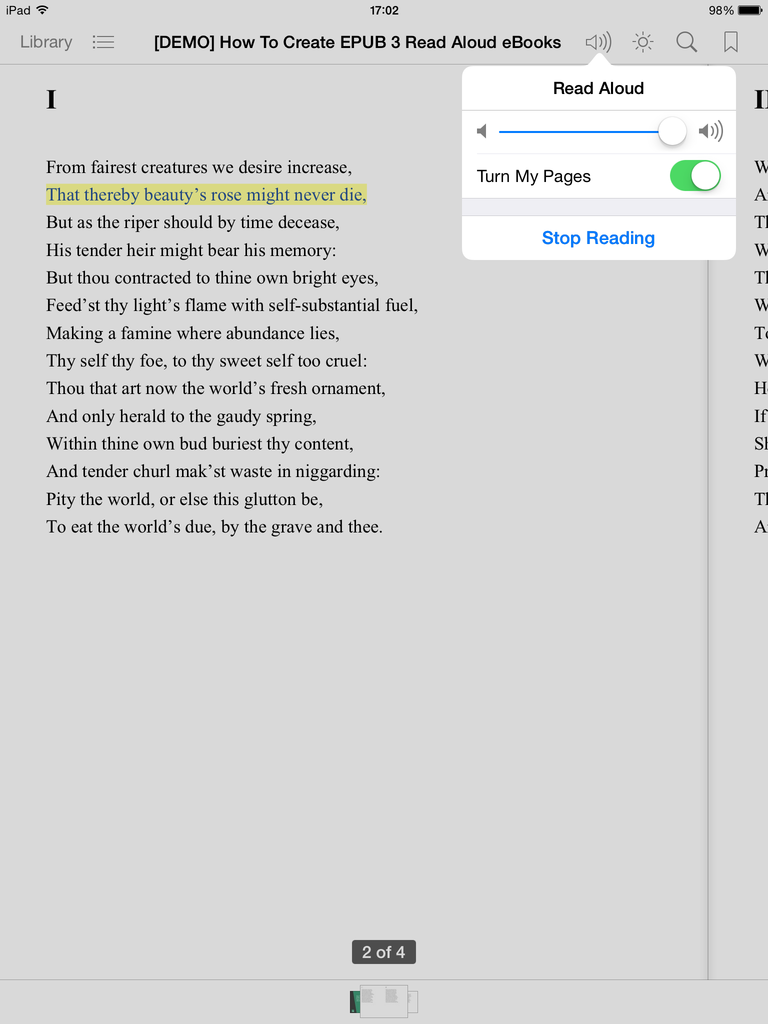
</package>If you want, you can download the resulting EPUB 3 file, released under the terms of the CC BY-NC-SA 4.0 license, and load it to e.g. iBooks:
(Note: no effort has been made to make this demo look "pretty"; after all, this demo is about MO, not CSS/FXL gimmicks. I chose to show a FXL sample because unfortunately MO are better supported for FXL eBooks, and ReadBeyond has plenty of reflowable EPUB 3 with MO eBooks freely available already.)